Pascal’s triangle

Time ago, I was introduced to solve Pascal’s triangle. For reference, see following link on Wikipedia. Technically is an interesting exercise for programmers, where functions and recursion comes into rescue.

Here is an image that helps better understand the Pascal’s triangle and how it’s created.

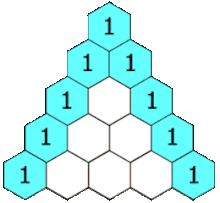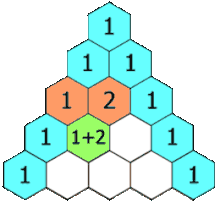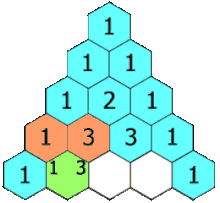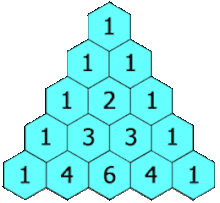
My algorithm is posted on this gist.

You can see below the code running in repl.it, press the Play button.

Approach

The core reasoning of my solution is to have the ability to calculate any position being displayed. I discarded the use of arrays, I just think they are not worth on this case.

I like the approach I use because it has been educational to use “recursion” again. See, there are 3 functions, but in the algorithm, only one function returns a value 1 (one); with that, it’s calculating any position requested.

By doing it the way I did, the algorithm can virtually calculate any number of lines you set. One disadvantage you will realize in a moment, it’s that absolutely each “previous” position has to be calculated.

Source Code

# what is Pascal's triangle?
# https://en.wikipedia.org/wiki/Pascal%27s_triangle

number_of_rows = 11

def print_triangle_row(rows:int, current_row:int):
 
  one_line= ""

  # iterate on current_line
  for column in range(0,current_row):     
    value = calculate_position(rows,current_row,column)
    one_line += f"{value}\t"

  print(f"{one_line}")
  
  if current_row < rows:
    print_triangle_row(rows,1+current_row)
  else:
    return

def calculate_position(rows:int, current_row:int, current_column:int):
  if current_row <= 1 or current_column == 0 or current_column == (current_row-1):
    return 1

  return calculate_position(rows, current_row-1, current_column-1) + calculate_position(rows, current_row-1, current_column)

def pascal_triangle(rows:int):
  if rows > 0:
    print_triangle_row(rows,1)
  else:
    print("Error!")

pascal_triangle(number_of_rows)
print("terminamos...")

Have fun.